Coefficient of tail dependence of a
Clayton copula
[this page | pdf | back links]
Bivariate Archimedean copulas are copulas that take the
form 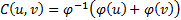 for
some suitable function
for
some suitable function 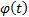 where
where 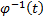 is the
inverse function of
is the
inverse function of 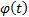 (not
its reciprocal). A special case is the Clayton copula, which has
(not
its reciprocal). A special case is the Clayton copula, which has 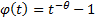 where
where 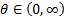 .
.
The coefficient of (joint lower) tail dependence is defined
as 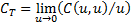 . For
the Clayton copula this can take any value in the range
. For
the Clayton copula this can take any value in the range 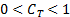 . This
is because
. This
is because 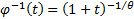 since
then (for
since
then (for 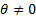 ):
):
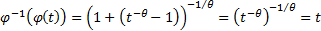
Hence the (bivariate) Clayton copula is: 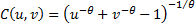 .
.
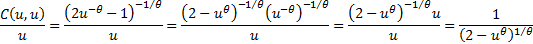
So the coefficient of (joint lower) tail dependence for the (bivariate)
Clayton copula is:
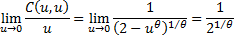
As 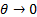 this
tends to 0 from above, and as
this
tends to 0 from above, and as 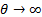 this
tends to 1 from below and can take any intermediate value, i.e. the range of
lower tail dependences that the Clayton copula can exhibit is the range (0,1).
this
tends to 1 from below and can take any intermediate value, i.e. the range of
lower tail dependences that the Clayton copula can exhibit is the range (0,1).
For an arbitrary copula the coefficient of tail dependence, 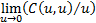 , can
in addition take the values 0 (e.g. the independence copula or any Gaussian
copula that does not involve perfect correlation) or 1 (e.g. perfectly
correlated Gaussian copula) or it may be ill-defined, i.e. it may not exist.
, can
in addition take the values 0 (e.g. the independence copula or any Gaussian
copula that does not involve perfect correlation) or 1 (e.g. perfectly
correlated Gaussian copula) or it may be ill-defined, i.e. it may not exist.