Moments of a binomial loss distribution
[this page | pdf | back links]
Suppose a portfolio has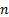 
equally-sized
exposures. Each one is independent and has a probability 
of
creating a unit loss (and a probability 
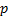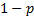of
creating a zero loss), with 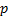the same
for each exposure, meaning that the portfolio loss,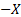 
,
is distributed according to a binomial distribution,
i.e.:
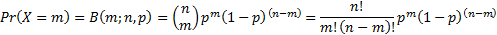
The mean and the variance of the portfolio loss distribution
can be found as follows. We note that:
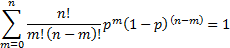
The mean of the loss distribution is given by:
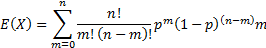
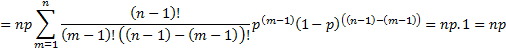
Likewise:
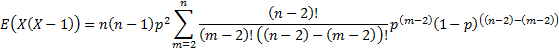
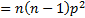
The variance of the loss distribution is:
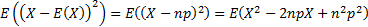
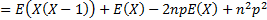
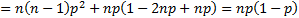
Thus binomial distribution has mean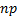 
and
variance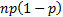 
.
As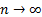 
, the
Central Limit Theorem CLT implies that the binomial distribution tends to a normal distribution
with the same mean and variance, i.e. to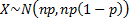 
where 
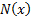is the
cumulative normal distribution.