ERM Glossary: Risk model
[this page | pdf | references | back links]
A (portfolio) risk model is
defined in Market
Consistency by M.H.D. Kemp as ‘a mathematical framework for estimating the
future spread of returns / outcomes a portfolio might generate were its
positions versus its benchmark to remain unaltered in the future’*.
More generally it is any
formulation of how risks might arise that is amenable to mathematical analysis.
Multivariate normal risk
models
A particularly simple mathematical
risk model is one in which the behaviour of future returns / outcomes is
characterised by a multivariate normal distribution with parameters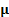 
(a vector of assumed
returns for each asset) and 
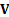(a covariance matrix).
Often in an asset management context
each element of 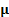would be assumed to be the same constant value (i.e. we do
not presume any ability to outperform the benchmark). Without loss of
generality this constant can be set equal to zero if we are focusing on returns
relative to a benchmark.
The easiest risk statistic that
can be derived from such a model is the (ex-ante) tracking error,
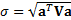where the 
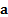correspond to the active positions versus the benchmark
(i.e. each element 
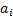of 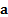is defined as 
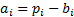, where 
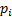is the weight of the 
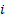’th security in the portfolio and 
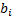is its weight in the benchmark).
For this model type, other risk
statistics such as Value-at-Risk
(VaR) for a given confidence level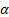 
can be derived from 
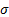by referring to the 
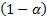quantile of a normal distribution with standard deviation 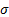. Such a VaR model is often called the variance-covariance
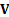VaR (particularly if is based on the historical covariance matrix of different
return series).
* Or, if the positions were to
change in any prespecified dynamical manner under consideration
NAVIGATION LINKS
Contents | Prev | Next