/

Enterprise Risk Management Formula Book

2. Series expansions (for real-valued functions)

[this page | pdf | back links]

2.1          Exponential function and natural logarithm (log) function

 

 

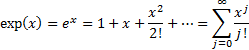
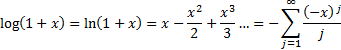
2.2          Binomial expansion

 

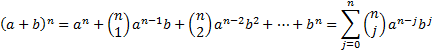
where 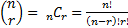 is the binomial coefficient.

 

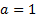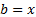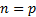If we substitute into the binomial expansion ,  and  we have (converges for any 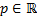 if ):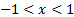

 

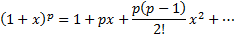
A corollary is that:

 

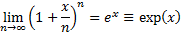
2.3          Taylor series expansion

 

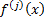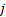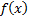For one variable: if series converges (where  is the ’th derivative of  and 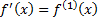,  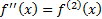etc.):

 

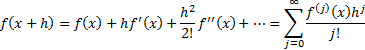
For more than one variable: e.g. for two variables, if series converges (where 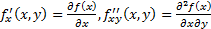  etc.):

 

 

---

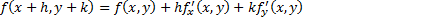
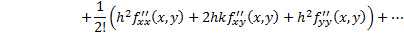
NAVIGATION LINKS
Contents | Prev | Next

---