Enterprise Risk Management Formula Book
8. Financial derivatives
[this page | pdf | back links]
8.1 Forward prices
The no arbitrage (fair) forward price which parties should
agree to exchange a security at time 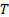 if it is
priced
if it is
priced 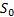 now and is
entitled to fixed income of present value
now and is
entitled to fixed income of present value 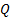 in the
meantime is:
in the
meantime is:
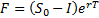
where 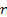 is the
interest rate (continuously compounded).
is the
interest rate (continuously compounded).
If instead it pays dividends at a rate 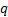 (continuously
compounded) then the forward prices is:
(continuously
compounded) then the forward prices is:
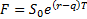
8.2 Black-Scholes formulae
Geometric Brownian motion for a security (stock) price 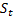 involves
involves
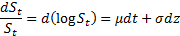
The partial differential equation satisfied by values of
payoffs involving such security prices is:
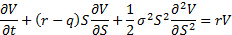
where 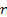 is the
interest rate,
is the
interest rate, 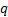 is the
dividend yield (both continuously compounded) and
is the
dividend yield (both continuously compounded) and 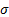 is
the security price volatility.
is
the security price volatility.
Garman-Kohlhagen formulae for values at time 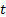 of
European-style put and call options with strike price
of
European-style put and call options with strike price 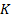 maturing
at time
maturing
at time 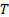 :
:
where
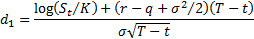
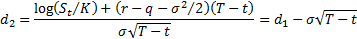
We then have 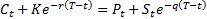 , i.e. put-call
parity.
, i.e. put-call
parity.
Technically the Black-Scholes formulae
are special cases of the Garman-Kohlhagen formulae for stocks that pay no
dividend, i.e. have 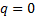 , although
in practice the two names are normally treated as interchangeable.
, although
in practice the two names are normally treated as interchangeable.
The Black-Scholes option pricing formulae can also be
derived as the limit of binomial trees (lattices) with movements 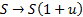 or
or 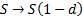 with an
up-step probability
with an
up-step probability 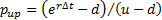 and a
down-step probability
and a
down-step probability 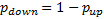 where:
where:
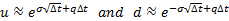
NAVIGATION LINKS
Contents | Prev | Next