Standard Statistical Tests for Normality:
The Cramér-von Mises test
[this page | pdf | back links]
See also Standard Statistical
Tests for Normality.
The Cramér-von Mises test tests the null hypothesis
that a sample,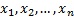 
comes
from a pre-specified population distribution (or a pre-specified family of such
distributions).
In its basic form, the test assumes that there are no
parameters to be estimated for the distribution being tested, in which case the
test and its set of critical values are distribution-free.
However, it is most commonly used where a family of
distributions are being tested. For example, we might be testing whether the
sample comes from a Normal distribution but without specifying in advance the
mean and standard deviation of that distribution. It then becomes necessary to
estimate the parameters on which the particular distribution depends and this
needs to be taken into account by adjusting the test statistic and/or its
critical values.
In its basic form, it involves the following test statistic,
,
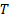where we are testing the null hypothesis that the data is coming from a
distribution with cumulative distribution function (cdf)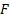 
:
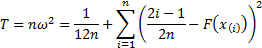
wher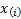e 
is
the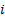 
’th order statistic, i.e. the 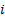’th smallest
value in the sample. If the empirical distribution function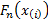 
is
defined as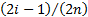 
then
the statistic can be seen to be (up to a constant for any given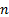 
) similar to
the statistic used in the Kolmogorov-Smirnov
test, but using the mean squared deviation rather than the supremum of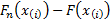 
.
Essentially the same approach can be used when testing
whether data comes from a pre-specified family of distributions.
However, the statistic must then be compared against critical values
appropriate to the family in question and dependent also on the method used for
parameter estimation.
Like the Kolmogorov-Smirnov
test, the test can also in principle be inverted to give confidence limits on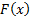 
itself
and a variant can be used to test whether two (or more) underlying
one-dimensional distributions differ. Generalising the statistic to more than
one dimension is possible but complicated.
NAVIGATION LINKS
Contents | Prev