Derivative Pricing – Cost of Capital
Pricing Model
[this page | pdf | references | back links]
1. A simple way of incorporating in derivative
pricing the possibility that investment markets might jump is to consider the
limiting (and therefore typically unrealistic) case where the price of the
underlying might jump to zero or infinity. This is the basis of the ‘cost of
capital’ developed by M.H.D. Kemp and A.D. Smith, see e.g. Kemp (1997) or
Kemp (2009).
2. This model assumes that in any small instant
the underlying may jump in price either infinitely upwards or down to zero. An
option writer is putting his or her capital at risk from such jumps as they are
not hedgeable by investing merely in the underlying and risk-free assets. It
is reasonable to assume that the option writer will demand an excess return on
the ‘risk capital’ that the option writer needs, to reflect this risk. Of
course, such risks can be hedged by buying suitable options, but this has
merely transferred the jump risk to someone else. Ultimately, someone must
carry this risk.
3. The model thus has two additional parameters
to those applicable to the Black-Scholes formulae, namely:
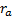 = the rate
of interest required on the cash the writer would need to hold to make good the
loss that he would incur if there were an extreme downward jump in the price of
the underlying shares and
= the rate
of interest required on the cash the writer would need to hold to make good the
loss that he would incur if there were an extreme downward jump in the price of
the underlying shares and
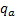 = the
enhanced income yield required on the shares the writer would need to hold to
make good the loss that he would incur if there were an extreme upward movement
in the price of the underlying shares
= the
enhanced income yield required on the shares the writer would need to hold to
make good the loss that he would incur if there were an extreme upward movement
in the price of the underlying shares
4. The values under this model of European put
options 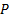 and call
options
and call
options 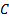 are as
follows, see Kemp
(1997) for a derivation. They bear some resemblance to the formulae
applicable in the more basic Black-Scholes world (and reproduce them in the
special case where
are as
follows, see Kemp
(1997) for a derivation. They bear some resemblance to the formulae
applicable in the more basic Black-Scholes world (and reproduce them in the
special case where 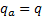 and
and 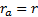 ).
).
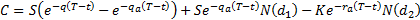
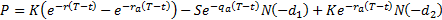
where:
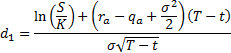
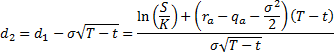
5. The Nematrian website includes functions for
pricing European call and put options given the ‘cost of capital’ model, namely
MnCCCall and MnCCPut respectively. The ‘CC’
here refers to the cost of capital model, to differentiate the pricing model
from the basic Black-Scholes model, designated within the Nematrian web
services toolkit by ‘BS’.