Continued Fractions
[this page | pdf | references | back links]
A continued fraction (characterising a function in
one variable) has the following form:
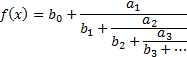
Publishers tend to prefer to write this as:
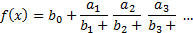
In either format the 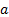 ’s
and
’s
and 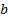 ’s can themselves be
functions of
’s can themselves be
functions of 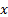 (usually linear or
quadratic at worst, i.e. low order polynomials in
(usually linear or
quadratic at worst, i.e. low order polynomials in 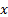 ).
).
Continued fractions are often powerful ways of numerical
evaluation of functions since they often converge much more rapidly than power
series expansions. According to Press et
al. (2007) they often also have a larger domain of convergence in the
complex plane, which means that they can prove an effective way of evaluating a
function for a wider range of input values than might be practical with a power
series expansion.