Constrained Quadratic Optimisation: 6.
Portfolio optimisation
[this page | pdf | references | back links]
Return to
Abstract and Contents
Next
page
6. Portfolio
optimisation
In a (mean-variance) portfolio optimisation context, the
objective that we typically want to maximise is the following (or some
monotonic equivalent):
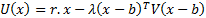
Here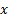 
are the
portfolio weights (so typically we impose at least the following constraint 
), 
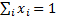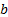is
the benchmark (or ‘minimum risk’ portfolio),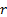 
is
a vector of assumed returns on each asset and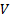 
is
the covariance matrix (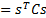
, where 
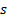is
the vector of risks on each asset class, here assumed to be characterised by their
volatilities, as this approach is merely a mean-variance one, and 
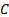their
correlation matrix).
NAVIGATION LINKS
Contents | Prev | Next