Constrained Quadratic Optimisation: 4. Updating the tableau

[this page | pdf | references | back links]

Return to Abstract and Contents

Next page

4.            Updating the tableau

We update the tableau iteratively (probably only up to some upper limit of number of iterations, in case there is an error in the computation), and we stop when there is no change to the tableau at a given iteration.

To do this we need to identify which variable ought ideally to enter the feasible solution, i.e. to become a ‘basic’ variable, and which variable it should replace, i.e. which one is ceasing to be a basic variable. We need to do these simultaneously, since the constraints mean that only certain combinations of variables can enter and leave at the same time.

This may be done by identifying the largest positive value of the ObjectiveRow for a column (variable) which is not currently basic (but only if either the current corresponding variable is non-basic, so that the joint constraint of the form value 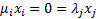 is still satisfied, or if the corresponding variable is basic then the two can be swapped over and still improve the objective function) and if there is another basic variable, which if removed from the feasible set at the same time improves the objective function.

As long as we identify a one entering basic variable (column) and one exiting basic variable (column) as above, we pivot the Tableau, ObjectiveRow and SolutionColumn around their intersection and we update the BasicRow and BasicColumn accordingly.

As mentioned above, sometimes we need to replace zeros with very small positive numbers to avoid the tableau becoming degenerate.

NAVIGATION LINKS
Contents | Prev | Next