The Nematrian Website’s Complex Number
Function Algorithms
[this page | pdf | back links]
The Nematrian website contains a suite of interactive pages
and web services that permit users to manipulate complex numbers. Complex
numbers are extensions to real numbers that historically owe their introduction
principally to attempts to solve algebraic equations, in the first instance the
equation 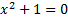 .
.
Each complex number has two components, its real part and
its imaginary part, and can thus be plotted in the so called complex plane
where the 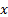 -coordinate refers to the
real part and the
-coordinate refers to the
real part and the 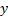 -coordinate refers to the
imaginary part of the complex number. Any real number can be considered to be a
complex number that has a zero imaginary part. Conventionally, a complex number
is written as, say,
-coordinate refers to the
imaginary part of the complex number. Any real number can be considered to be a
complex number that has a zero imaginary part. Conventionally, a complex number
is written as, say, 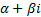 , where
, where 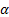 is its
real part, and
is its
real part, and 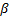 is its imaginary part, and
is its imaginary part, and
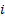 is
a purely complex number defined to be the square root of
is
a purely complex number defined to be the square root of 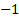 that
has positive imaginary part (to distinguish it from
that
has positive imaginary part (to distinguish it from 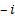 which
is also then a square root of
which
is also then a square root of 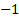 ). Complex numbers adhere
to the following extensions to the usual rules for adding, subtracting,
multiplying and dividing real numbers:
). Complex numbers adhere
to the following extensions to the usual rules for adding, subtracting,
multiplying and dividing real numbers:
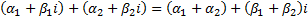
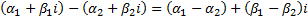
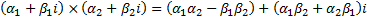
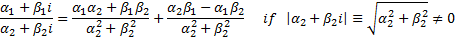
Any polynomial equation of order 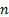 (>0),
i.e. of the form
(>0),
i.e. of the form 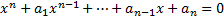 (where
the
(where
the 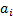 are
either real or complex) in general has
are
either real or complex) in general has 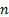 roots,
i.e. solutions, some of which may be real and some of which may be complex
(although not all of these roots are necessarily distinct). Large parts of the
mathematical theory of real analysis carry over to the complex case, indeed in
many instances introduction of complex number theory simplifies and streamlines
these results, e.g. the theory of analytic functions.
roots,
i.e. solutions, some of which may be real and some of which may be complex
(although not all of these roots are necessarily distinct). Large parts of the
mathematical theory of real analysis carry over to the complex case, indeed in
many instances introduction of complex number theory simplifies and streamlines
these results, e.g. the theory of analytic functions.
The functions (web services) that the Nematrian makes
available for manipulation of complex numbers are described further in ComplexNumbersFunctions.
To pass complex values to these web services, each number
that would otherwise have been a single ‘real’ variable needs to be replaced by
two numbers, the first being the real part of the complex number and the second
part of the complex number. Thus, if the equivalent real function expected a
single real number (typically a ‘double precision’ number using computer
algorithm terminology) then the corresponding Nematrian function taking a
complex number argument would expect to receive an array of two such numbers.
If the equivalent real function expected an array of real numbers then the
corresponding Nematrian function taking a complex number array argument would
expect to receive an array of twice the size, with the first and second
elements of the array being the real and imaginary parts of the corresponding
first element of the real number equivalent, the third and fourth corresponding
to the second element of the real number equivalent etc.
Some complex functions can be multivalued. For example, 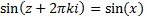 for
all real (or complex)
for
all real (or complex) 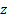 and integral
and integral 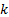 . Thus a
function such as
. Thus a
function such as 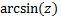 ,
i.e. the value
,
i.e. the value 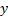 for which
for which 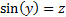 ,
does not in general have a unique value. Instead, it is usual for complex
number function algorithms to focus merely on the principal value of the
number, typically taken to mean the one for which choice of
,
does not in general have a unique value. Instead, it is usual for complex
number function algorithms to focus merely on the principal value of the
number, typically taken to mean the one for which choice of 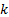 gives
the smallest absolute size for the imaginary part of the answer.
gives
the smallest absolute size for the imaginary part of the answer.