Coherent Risk Measures
[this page | pdf | references | back links]
A risk measure,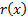 
is
defined by Artzner et al. (1999) to be coherent if it satisfies the following 4
axioms:
(a) Subadditivity:
for any pair of loss variables,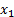 
and
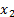
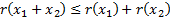
(b) Monotonicity:
if, for all states of the world,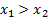 
then
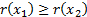
(c) Homogeneity:
for any constant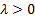 
and random loss variable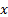 
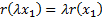
(d) Translational
invariance: for any constant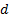 
and random loss variable
x
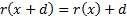
Artzner et
al. (1999) also showed that a risk measure is coherent if and only if there
is a family,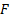 
, of probability measures,
,
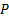such that:
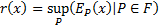
Sometimes the easiest way of proving that a risk measure is
coherent is to prove each of the four axioms are satisfied, at other times it
is easiest to show that it may be expressed in this supremum form.
For example TVaR can be shown to
be coherent by defining a set of probability measures that place equal
probability on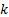 
realisations where 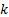is the
smallest integer such that 
.
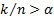TVaR is then the maximum expected value of losses over this family of
distributions.
In contrast, VaR is coherent only for a
limited class of distributions, including multi-variate Normal (i.e. Gaussian)
distributions (for proof see here)
and more generally for elliptical
distributions.