Calibrating probability distributions
used for risk measurement purposes to market-implied data: 3. Other comments
[this page | pdf | references | back links]
Return
to Abstract and Contents
Appendix
3. Other comments
3.1 If 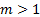 then the
simultaneous equations generated by the above procedure do not appear to have
analytic solutions, see e.g. the Appendix.
Instead they must in general be solved numerically by some iterative root
search algorithm, e.g. one that finds the value of
then the
simultaneous equations generated by the above procedure do not appear to have
analytic solutions, see e.g. the Appendix.
Instead they must in general be solved numerically by some iterative root
search algorithm, e.g. one that finds the value of 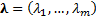 that
satisfies the following equation:
that
satisfies the following equation:
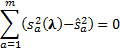
where:
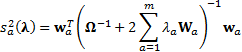
If the problem involves a relatively small number of
instruments/calibration implieds then the problem can be solved using
relatively straightforward tools such as the Excel Solver add-in. For larger
instrument universes and/or calibration sets, more sophisticated root searching
algorithms may be needed.
3.2 However, it may not always be appropriate to
adopt a rote formulaic approach to calibration. For example, suppose we were
trying to calibrate a UK equity risk model. Easily observable implied volatilities
are available from listed equity derivatives on the FTSE100 index, the FTSE250
index but only for an incomplete range of individual equities. What should we
do for securities for which there are no readily available implied
volatilities?
3.3 The problem of incomplete or missing data is,
of course, a generic problem with calibration, and not specific to the above
problem. We could of course calibrate solely to those instrument volatilities
that are easily observable. However, this would typically disproportionately
affect the volatility assigned to the instruments included in the calibration
set, see Appendix. Suppose that in fact general levels of implied volatilities
are materially higher than those in the uncalibrated prior distribution, e.g.
because there is an overall perception within the market that the “world is
uncertain at the moment”. Would we want calibration disproportionately to mark
up volatilities of securities on which there were readily available option
prices versus those on which there were not?
3.4 An alternative would perhaps be to introduce
just two 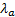 ’s, i.e.
two calibration equations. One might calibrate the volatility of the main
market index to its current implied volatility (or actually in the spirit of
above the variance to its current implied variance). The other might calibrate
the average volatility (variance) of individual instruments to the average of
their individual implied volatilities (variances) to the extent that these
exist, with the same overall volatility (variance) adjustment then also applied
to instruments where there is no observable implied volatility. Or perhaps we
could adopt an intermediate approach of applying averaging within individual
sectors rather than across the market as a whole. Of course, such averaging
approaches would be less effective at calibrating individual instrument
volatilities so that they exactly matched their own implied volatilities where
these exist. That is the nature of averaging! We might also want to impose
further constraints on the calibration to force retention of any parsimonious
factor structure imposed on the prior distribution.
’s, i.e.
two calibration equations. One might calibrate the volatility of the main
market index to its current implied volatility (or actually in the spirit of
above the variance to its current implied variance). The other might calibrate
the average volatility (variance) of individual instruments to the average of
their individual implied volatilities (variances) to the extent that these
exist, with the same overall volatility (variance) adjustment then also applied
to instruments where there is no observable implied volatility. Or perhaps we
could adopt an intermediate approach of applying averaging within individual
sectors rather than across the market as a whole. Of course, such averaging
approaches would be less effective at calibrating individual instrument
volatilities so that they exactly matched their own implied volatilities where
these exist. That is the nature of averaging! We might also want to impose
further constraints on the calibration to force retention of any parsimonious
factor structure imposed on the prior distribution.
3.5 Analytical weighted Monte Carlo can also be
used to calibrate risk models to cater for different future time periods, as
long as there is a suitable term structure of implied volatilities available.
We merely need to repeat the exercise separately for each term. Again, if
necessary, ‘missing’ calibration data can be handled using averaging approaches
as per 3.4.
3.6 It is worth noting that calibration of risk
models to market implieds may make resulting ex ante tracking errors, VaR’s and
other similar risk measures more volatile (because implied volatilities are
themselves volatile over even quite short periods of time). This may be
important if explicit ex ante tracking error or VaR style risk limits are
present in investment management agreements. Use of risk statistics calibrated
to market implieds might then create greater likelihood of breach of such
mandate restrictions merely because of market movements. We could dampen the
impact of this ‘volatility of volatility’ by applying some sort of credibility
weighting to current implied volatilities versus volatilities extrapolated from
past history but of course only at the expense of calibration quality.
Alternatively, it might be appropriate to quote more than one set of risk
statistics, e.g. some ‘longer term’ ones (perhaps based solely on extrapolating
past history using a relatively long time window) and some ‘shorter-term’ ones
more fully calibrated to market implieds. The former might then be used more
for mandate limit purposes and the latter more for day-to-day management of the
portfolio.
NAVIGATION LINKS
Contents | Prev | Next