Calibrating probability distributions
used for risk measurement purposes to market-implied data: 2. Multi-instrument
calibration – Section Conclusion
[this page | pdf | references | back links]
Return
to Abstract and Contents
Next
Section
2.5 What in practice does this mean in the
n-instrument case? Suppose we wish to calibrate to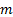 
different
variances 
(
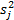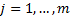) exhibited
by instrument baskets described by vectors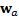 
, where
each 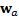is a
vector of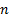 
elements,
the first element of which is the weight in the basket of the first instrument
etc. For example, suppose we have implied volatilities for each instrument in
isolation and for an equally weighted portfolio of the instruments. We would
then have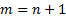 
calibrations,
the first 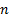of
which involve weight vectors of the form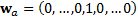 
(with
the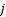 
’th
element of the weight vector being 1, other terms being zero) and the last
calibration having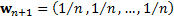 
. If
instead of calibrating to the implied volatility of an equally weighted basket
we wished to calibrate to the implied volatility of a market cap weighted index
implied volatility then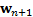 
would
be a vector of index weights.
2.6 The calibrated probability distribution will
then have a covariance matrix as follows, where each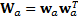 
is an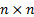 
dimensional
matrix:
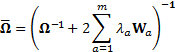
subject to the 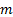calibration
equations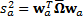 
.
2.7 As long as this problem is not ill posed (e.g.
because there are too many calibrations relative to the number of terms in the
covariance matrix, or because there are no feasible solutions to the equations)
calibration involves solving a set of 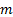simultaneous
equations 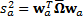in 
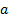unknowns,
i.e. the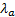 
.
2.8 An example of such a calibration is set out in
the Appendix.
{/CalibratingPriorsToMarketImpliedData2c}
NAVIGATION LINKS
Contents | Prev | Next