Calibrating probability distributions
used for risk measurement purposes to market-implied data: 1. Introduction
[this page | pdf | references | back links]
Return
to Abstract and Contents
Next
Section
1. Introduction
1.1 Kemp (2005)
and Kemp (2009)
argue in favour of greater use of market-consistent
risk management. This involves greater focus on market implied probability
distributions and other risk parameters (consistent with the market prices of
derivatives that might protect against the relevant risks) and lesser focus on
estimating such parameters using time series analysis of historic market
behaviour.
1.2 In practice, as is explained in Kemp (2009),
there is insufficient market implied data available to be able to build up a full
specification of the relevant market implied probability distribution. However,
there is often some market implied data that we can use for calibration
purposes. We explain in these pages how we can combine this data with an
assumed prior distribution in a Bayesian or credibility-weighted type manner,
thereby deriving risk measures that are as market consistent as possible, but
still coloured by our prior views in cases where market implied data does not exist.
A natural prior to adopt in this context, if we think the historic data is
relevant, is one based on the relevant historic dataset.
1.3 A prototype methodology for market consistent
risk measurement is described in Kemp (2009)
involving an analytical weighted Monte Carlo, aka analytical relative
entropy approach. This involves identifying a distribution that is, in some
suitable sense, as ‘close as possible’ to the original prior distribution but
that has characteristics that match calibration characteristics derived from
market implied data (or otherwise).
1.4 As its name suggests, the analytical weighted
Monte Carlo methodology has its genesis in the weighted Monte Carlo simulation
approach, see Elices
& Gimenez (2006) and Avellandeda
et al (2001). In this approach, we calibrate a simulation exercise not by
changing the draws from some previously specified prior probability
distribution but by changing the assumed likelihoods ascribed to each draw in
the computation of statistics in which we are interested (e.g. mean, standard
deviation, other moments, quantiles etc.). Typically we choose these revised
likelihoods of occurrence to minimise the relative entropy between the
original prior distribution and the calibrated output distribution. The
relative entropy between two discrete distributions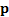 
and 
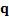is given
by the following, where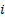 
here
indexes the possible outcomes (the formula for continuous distributions is
derived in an analogous manner):
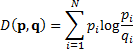
1.5 The analytical weighted Monte Carlo methodology
notes that in the limit where the number of simulations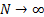 
we will
recover an exact output probability distribution and that in a number of cases
of interest this probability distribution can be expressed in ‘analytical’
form, i.e. we may be able to recover relatively simply what the methodology
would have produced had we been able to use an infinitely large Monte Carlo
sample size.
1.6 In the special case of single instrument
calibration involving a univariate normal prior distribution, say,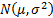 
we find,
as we might expect, that application of an analytical weighted Monte Carlo
returns a normal distribution with the following characteristics, see Kemp (2009):
(a) If we have no
market data whatsoever to calibrate to then the calibrated distribution is the
same as the prior distribution, i.e. ;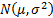
(b) If we have just a mean
to calibrate to, say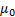 
, then
the calibrated distribution is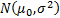 
; and
(c) If we have both
a mean and a variance to calibrate to, say, 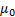and 
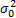, then
the calibrated distribution is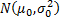 
.
For risk management purposes, it is usual to adopt the
assumption that the return on all assets is the same (i.e. to discount the
possibility of ‘manager skill’, because it is prudent to do so). It can be
argued that (b) provides the theoretical justification for this, i.e. in effect
we are ‘calibrating’ some assumed prior distribution (that might include
differential returns) to fit a constraint that requires any prior assumed
manager skill in asset selection not actually to be present in practice.Without
loss of generality the mean return can for the purposes of this paper be set to
zero (since our focus will be on relative returns). Hence our focus will be on
second and higher moments (or just second moments in the case of normally
distributed variables, which is the main focus of these pages).
NAVIGATION LINKS
Contents | Prev | Next