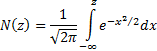Deriving the Black-Scholes Option Pricing
Formulae using Ito (stochastic) calculus and partial differential equations
[this page | pdf | references | back links]
The following partial differential equation is satisfied by
the price of any derivative on  , given the assumptions
underlying the Black-Scholes world:
, given the assumptions
underlying the Black-Scholes world:
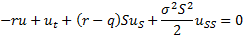
This partial differential equation is a second-order, linear
partial differential equation of the parabolic type. This type of
equation is the same as used by physicists to describe diffusion of heat. For
this reason, Gauss-Weiner or Brownian processes are also often commonly called diffusion
processes.
If  ,
, 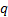 and
and 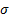 are
constant then we can solve it by transforming it into a standard form which
others have previously solved, namely (for some constant
are
constant then we can solve it by transforming it into a standard form which
others have previously solved, namely (for some constant 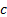 ):
):
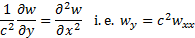
This can be achieved by replacing 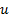 by
by 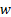 where
where
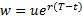 (as long as
(as long as 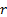 is
constant) and by making the following double transformation (assuming that
is
constant) and by making the following double transformation (assuming that 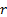 ,
, 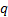 and
and 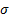 are
constant):
are
constant):
This transformation removes one of the terms in the partial
differential equation:
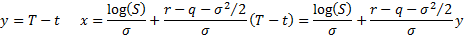
The partial differential equation then simplifies to 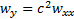 , with
, with 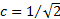 . Prices of different
derivatives all satisfy this equation and are differentiated by the imposition
of different boundary conditions. A common tool for solving partial
differential equations subject to such boundary conditions is the use of Green’s
functions. This expresses the solution to a partial differential equation
given a general boundary condition applicable at some boundary
. Prices of different
derivatives all satisfy this equation and are differentiated by the imposition
of different boundary conditions. A common tool for solving partial
differential equations subject to such boundary conditions is the use of Green’s
functions. This expresses the solution to a partial differential equation
given a general boundary condition applicable at some boundary 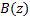 , formed say by the
curve
, formed say by the
curve 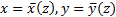 , as an expression of
the following form, in which
, as an expression of
the following form, in which 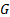 is called the Green’s
function for that partial differential equation:
is called the Green’s
function for that partial differential equation:
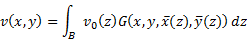
The Green’s function for 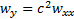 where
where 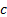 is
constant is:
is
constant is:
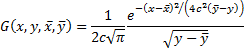
If the boundary condition is expressed as 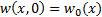 at
at 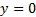 , where
, where 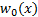 is continuous and
bounded for all
is continuous and
bounded for all 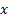 , then the solution is:
, then the solution is:
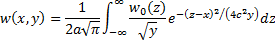
For a European call option, with strike price 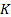 , we
have, after making the substitutions described above,
, we
have, after making the substitutions described above, 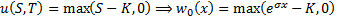 . After some further
substitutions we find that this implies that:
. After some further
substitutions we find that this implies that:
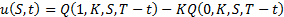
where:
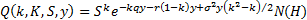
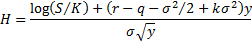
Substituting 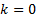 and
and 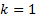 into the formula for
into the formula for 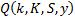 recovers the
Black-Scholes formulae, e.g. for a call option:
recovers the
Black-Scholes formulae, e.g. for a call option:
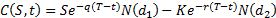
Where
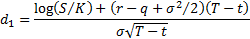
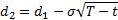
and 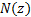 is the cumulative
Normal distribution function, i.e.
is the cumulative
Normal distribution function, i.e.