Valuing polynomial payoffs in a Black
Scholes World
[this page | pdf | back links]
If the price of the underlying follows a Gauss-Weiner
process (as is the case in the Black-Scholes world) then valuation of a
derivative relating to a European-style payoff would appear to involve
calculating the following integral, where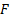 
is the payoff
function:
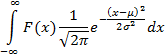
Any payoff can be approximated arbitrarily accurately using
combinations of piecewise polynomials. Even payoffs with discontinuities (e.g.
digital options) can be approximated by combinations of value functions and
(multiple) indicator pairs, where the pairs define the domain over which the
relevant payoff function applies.
However, it is important to realise that prior to the
representation of the pricing problem in the above format there is a
transformation of variables that complicates how in practice this integral
should best be evaluated.
The partial differential equation satisfied by any
derivative in a Black-Scholes world is:
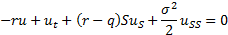
We can convert this equation into a standard form with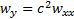 
using the
following transformations:
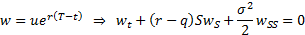
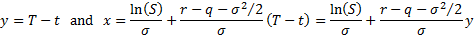
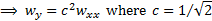
To value European style payoffs we need to solve an initial
value or Cauchy problem. If the boundary condition is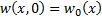 
at 
,
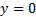where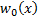 
is continuous
and bounded for all 
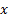then the solution
becomes:
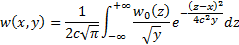
Suppose that the payoff has the following general form:
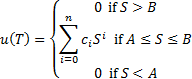
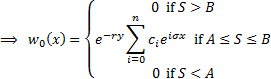
The solution to the pricing problem is thus:
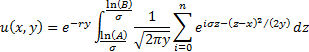
The original polynomial elements in the payoff function are
thus transformed into exponential terms in final integral representation.