Archimedean copulas
[this page | back links]
A copula
is a specialised form of multivariate probability distribution that has uniform
marginals (technically the copula is the cumulative distribution function of
such a distribution). In practice, researchers tend either to use:
(a) Copulas
implicitly derived from well-known multivariate distributions, e.g. the Gaussian copula (which
is the copula applicable to multivariate normal, i.e. Gaussian, distributions)
or the t copula (which
is the copula applicable to multivariate t distributions); or
(b) Simpler explicit
copulas that depend on a handful of parameters, often just one.
Any multivariate distribution can in principle be the source
of a copula; all we need to do is rescale the individual random variables so
that they each have uniform marginal distributions. Copulas derived in this
manner are called implicit copulas. The Gaussian copula is an example of
such a copula.
Simpler copulas tend to be explicit, i.e. to be
specifically defined by reference to the form of their copula. Examples include
the following (where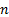 
is the dimension of the
multivariate distribution):
* The countermonotonicity copula is only defined for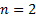 
.
Many of the copulas tabulated above are Archimedean
copulas. These are copulas which take the form:
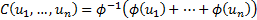
Here,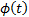 
is
called the generator function of the Archimedean copula and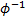 
is
its inverse function. In some instances, (e.g. when we extend the range
of the Clayton copula to include values for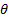 
to
include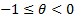 
) we need to replace 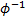in
the above by the pseudo-inverse,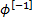 
.
Suppose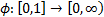 
is
a continuous strictly decreasing function that maps the interval 0 to 1 onto
the non-negative real line and has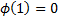 
and
.
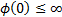Then its pseudo-inverse is defined as:
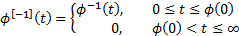
A strict generator is one that has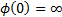 
,
i.e. where the pseudo inverse function is the inverse function.
A bivariate copula (i.e. with 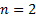) defined
as above is a copula if and only if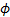 
is convex. A necessary
condition for a multivariate Archimedean copula (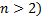
defined as
above to be a copula is that the generator is strict. It also needs to have its
generator inverse being completely monotonic. A decreasing function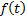 
is
completely monotonic on the interval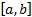 
if
it satisfies:
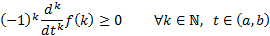
A bivariate Archimdean copula has a Kendall’s tau,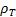 
,
as follows:
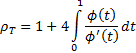
Where the copula depends on just one parameter then this
allows the parameter to be estimated from observed data.
The Archimedean copulas described above are exchangeable,
by which is meant that they have the same structural form if we swap different
dimensions around, since e.g.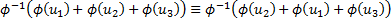 
etc.
Bivariate Archimedean copulas are often used in modelling
applications. However, as the number of dimensions increases it becomes
increasingly implausible that the ‘true’ dependency structure should be
exchangeable across all possible variables simultaneously. A number of
refinements have been proposed that include some but not complete
exchangeability, see e.g. McNeil et
al. (2005).