Annualisation Conventions: 2. ‘Interest’
rates vs ‘discount’ rates
[this page | pdf | back links]
Return to
Overview
Next section
In some circumstances,
yields are not quoted in the form of interest rates but in the form of discount
rates. Usually, ‘discount rate’ is used synonymously with ‘interest rate’,
as a tool for calculating present values of future cash flows. However, in
older literature the two terms may be distinguished, with discount rates being
the way in which interest rates are traditionally quoted on discount bills. In
such usage ‘discount rates’ would be expressed as fractions or percentages of
the final terminal amount, rather than as fractions or percentages of the
initial investment. So, if we invest 90 for one year and the terminal amount is
100 then the discount rate (with annual compounding), using this terminology,
is 10%. More generally, if an amount 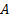 is invested for
is invested for 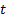 years
at a discount rate, using this terminology, of
years
at a discount rate, using this terminology, of 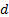 that
is compounded
that
is compounded 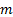 times per annum then
the terminal value of an investment is:
times per annum then
the terminal value of an investment is:
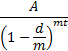
Again we may consider the
limit, as 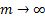 . We find that the
continuously compounded discount rate, using this terminology, is the same as
the continuously compounded interest rate, since
. We find that the
continuously compounded discount rate, using this terminology, is the same as
the continuously compounded interest rate, since 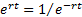 .
.
In actuarial texts, the
‘effective’ interest and discount rates (i.e. annually compounded) are
sometimes referred to by 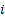 and
and 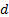 respectively
and the ‘nominal’ interest and discount rates (compounded
respectively
and the ‘nominal’ interest and discount rates (compounded 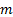 times
per annum) are sometimes referred to by
times
per annum) are sometimes referred to by 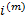 and
and 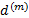 respectively (in
older texts,
respectively (in
older texts, 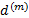 is sometimes instead
referred to by
is sometimes instead
referred to by 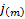 ). The ‘force’ of
interest and the ‘force’ of discount (i.e. the continuously compounded rates)
are the same and are sometimes referred to by
). The ‘force’ of
interest and the ‘force’ of discount (i.e. the continuously compounded rates)
are the same and are sometimes referred to by 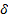 .
We then have the following relationships.
.
We then have the following relationships.
|
|
Effective interest rate
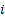
|
Nominal rate of
interest 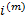
|
Effective rate of
discount 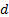
|
Nominal rate of
discount 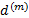
|
Force of interest or
discount 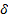
|
|
Value of 1 after time 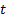
|
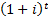
|
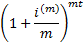
|
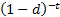
|
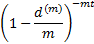
|
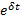
|
|
Present value of 1 due
after time 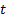
|
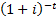
|
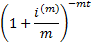
|
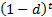
|
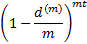
|
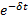
|
NAVIGATION LINKS
Contents | Prev | Next