Annualisation Conventions: 1.
Introduction
[this page | pdf | back links]
Return to
Overview
Next section
A statement from a bank
or insurer that a deposit will be credited with interest at the rate of 10% per
annum may sound unambiguous. In fact it is not. Interest rates and yields (and
hence spreads between different interest rates) can be quoted in a variety of
ways.
First we note that market
interest rate levels will differ according to the term of the deposit. Thus in
practice we might find that the interest rate credited on 1 year deposits is 5%
per annum, but on 2 year deposits is 6% per annum, say. This dependency on time
is called the ‘yield curve’. Interest bearing bonds will have a ‘running’ (or
‘coupon’) yield, which is the interest per unit nominal received each year.
However, as their price may not be at par, attention is more usually focused on
their ‘redemption yield’, i.e. the rate of return needed to equate their
current value with the present value of all future payments, both income and
redemption proceeds. With equities, which pay uncertain levels of dividends,
the ‘dividend yield’ may refer to the current dividend rate divided by the
current price. The ‘rental yield’ is a corresponding term that is used for
property, i.e. real estate, referring here to the rental income that the
property might provide. All of the above may be quoted gross or net of tax if
relevant (and potentially also gross or net of other types of expenses).
However these various
definitions of yield still do not exhaust the range of meanings that can be
placed on a quoted interest rate. In particular, the meaning to be ascribed to
any particular interest rate depends on the ‘annualisation convention’ being
adopted.
If, say, a 10% per annum
interest rate is being quoted with annual compounding the statement
that the interest rate is 10% per annum means that at the end of one year 100
grows to:
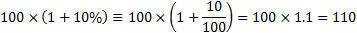
To be meaningful we of
course also need to specify the currency (or more generally the ‘numeraire’) in
which value is being expressed, e.g. US$, GB£, Euro, Yen, ....
However, when the
interest rate is expressed with semi-annual compounding, then the
statement means that we earn 5% every six months. This means that at the end of
one year 100 grows to:
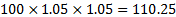
When the interest rate is
expressed with quarterly compounding, then the statement means that we
earn 2.5% every 3 months. This means that at the end of one year 100 grows to:
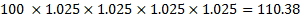
We can generalise these
results by supposing that an amount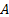 
is invested for 
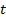years
at an interest rate of 
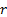that is compounded 
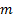times
per annum. The terminal value of the investment is then:
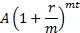
The limit as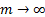 
is
called continuous compounding. The terminal value is then:
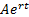
Here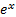 
, also called 
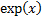or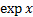 
, is the exponential
function, i.e.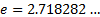 
raised to the power
of 
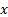. The continuously
compounded interest rate (sometimes also called the force of interest)
equivalent to a 10% annually compounded interest rate is thus:
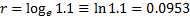
The difference between
interest rates quoted with different annualisation conventions increases the
further the interest rate deviates from 0%, as is illustrated in Table 1. For
most practical purposes, continuous compounding can be thought of as equivalent
to daily compounding.
NAVIGATION LINKS
Contents | Prev | Next