Standard Statistical Tests for Normality:
The Anderson-Darling test
[this page | pdf | references | back links]
See also Standard Statistical
Tests for Normality.
The Anderson-Darling test tests the null hypothesis
that a sample,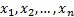 
comes
from a pre-specified population distribution (or a pre-specified family of such
distributions).
In its basic form, the test assumes that there are no
parameters to be estimated for the distribution being tested, in which case the
test and its set of critical values are distribution-free.
However, it is most commonly used where a family of
distributions are being tested. For example, we might be testing whether the
sample comes from a Normal distribution but without specifying in advance the
mean and standard deviation of that distribution. It then becomes necessary to
estimate the parameters on which the particular distribution depends and this
needs to be taken into account by adjusting the test statistic and/or its
critical values.
The test was published in 1952, see Anderson
and Darling (1952). It is based on the observation that if the data does
come from the hypothesised distribution then the data can be transformed to
what should be a uniform distribution. The transformed data can then be tested
for uniformity with a distance test, see e.g. Shapiro (1980).
In its basic form, it involves the following test statistic,
,
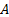where we are testing the null hypothesis that the data is coming from a
distribution with cumulative distribution function (cdf)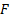 
:
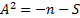
wher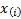e 
is
the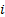 
’th order statistic, i.e. the 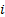’th smallest
value in the sample and
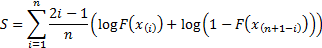
Essentially the same approach can be used when testing
whether data comes from a pre-specified family of distributions.
However, the statistic must then be compared against critical values
appropriate to the family in question and dependent also on the method used for
parameter estimation.
A ‘K-sample’ Anderson-Darling test can be used to
test whether several samples appear to be coming from a single distribution,
without the need to specify in advance what the distributional form might be. Sholz and
Stephens (1987) indicate how this basic approach can be used to test
whether a number of random samples with possibly different sample sizes are
coming from the same underlying distribution, where this distribution is
unspecified in advance.
NAVIGATION LINKS
Contents | Prev | Next