The Akaike Information Criterion
[this page | pdf | references | back links]
The Akaike Information Criterion is one of a range of ways
of choosing between different types of models that seek an appropriate
trade-off between goodness of fit and model complexity. The more complicated a
model is the better generally will be its apparent goodness of fit, if the
parameters are selected to optimise goodness of fit, but this does not
necessarily make it a ‘better’ model overall for identifying how new data might
behave.
A simple example of this is that if we have 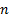 datapoints,
i.e.
datapoints,
i.e. 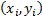 for
for 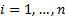 ,
relating to some unknown function then we can exactly fit all of these points
with a polynomial of order
,
relating to some unknown function then we can exactly fit all of these points
with a polynomial of order 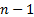 , i.e.
, i.e. 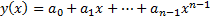 where the
where the 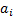 are fixed, but a
smoother polynomial with lower order or some other function with few parameters
may actually be a better guide as to what the value of
are fixed, but a
smoother polynomial with lower order or some other function with few parameters
may actually be a better guide as to what the value of 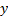 might
be for the
might
be for the 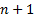 ’th datapoint even
though it is unlikely to fit the first
’th datapoint even
though it is unlikely to fit the first 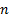 points as well as
the exact fit polynomial of order
points as well as
the exact fit polynomial of order 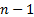 .
.
As explained in e.g. Billah,
Hyndman and Koehler (2003), a common way of handling this trade-off in the
context of statistics is to choose the model (out of say 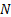 model
types, each of which is characterised by a vector of the
model
types, each of which is characterised by a vector of the 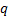 unknown
free parameters where
unknown
free parameters where 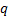 varies between the
different model types) that provides the highest ‘information criterion’ of the
form:
varies between the
different model types) that provides the highest ‘information criterion’ of the
form:
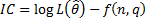
where 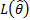 is the maximised
log-likelihood function,
is the maximised
log-likelihood function, 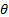 is the vector of
the
is the vector of
the 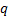 unknown free
parameters within the relevant model,
unknown free
parameters within the relevant model, 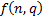 is a penalty
function that penalises more complex models and we are using a data series of
length
is a penalty
function that penalises more complex models and we are using a data series of
length 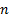 for fitting
purposes.
for fitting
purposes.
A range of information criteria have been proposed for this
purpose including:
|
Criterion
|
Penalty function
|
|
AIC (Akaike’s Information Criterion)
|
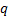
|
|
BIC (Bayesian Information Criterion)
|
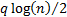
|
|
HQ (Hannan & Quinn’s Criterion)
|
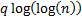
|
|
MCp (Mallow’s Criterion)
|
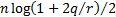
|
|
GCV (Generalized Cross Validation Criterion)
|
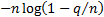
|
|
FPE (Finite Prediction Error Criterion)
|
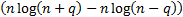
|
where (for MCp) 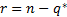 and
and 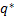 is the number of
free parameters in the smallest model that nests all models under
consideration. Billah, Hyndman and Koehler’s innovation is seek to estimate an
‘ideal’
is the number of
free parameters in the smallest model that nests all models under
consideration. Billah, Hyndman and Koehler’s innovation is seek to estimate an
‘ideal’ 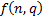 for the purpose in
hand, thus deriving an ‘empirical’ information criterion rather than
necessarily adopting a fixed penalty functional form.
for the purpose in
hand, thus deriving an ‘empirical’ information criterion rather than
necessarily adopting a fixed penalty functional form.