Accelerated Convergence Techniques
[this page | pdf | references | back links]
The term accelerated convergence appears in a number
of different guises in mathematics and finance.
1. In the context of numerical integration
(also called quadrature), accelerated convergence can relate to
approaches that aim to converge more rapidly to the correct answer as the number
of evaluations, 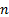 , of the
underlying function increases.
, of the
underlying function increases.
Perhaps the most important example is what is more
classically known as Simpson’s rule. The theory can be developed as follows.
The simplest and perhaps most obvious way of evaluating an integral numerically
is the so-called trapezoidal rule. Suppose we are trying to evaluate 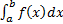 and the
abscissas (i.e. the points at which the function is evaluated) are equally
spaced, say at
and the
abscissas (i.e. the points at which the function is evaluated) are equally
spaced, say at 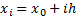 for
for 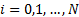 (so
(so
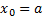 and
and 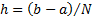 ), with the
values of
), with the
values of 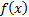 there being
there being 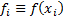 . The
trapezoidal rule involves approximating the integral by the following formula:
. The
trapezoidal rule involves approximating the integral by the following formula:
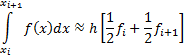
The accuracy of this approximation can be expressed as
follows:
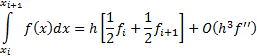
By 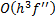 we mean that
the true answer differs from the estimate by an amount that is the product of
some numerical coefficient times
we mean that
the true answer differs from the estimate by an amount that is the product of
some numerical coefficient times 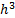 times the
value of the second derivative of the function somewhere in the interval of the
integration (assuming that the function is sufficiently smooth and actually has
a second derivative).
times the
value of the second derivative of the function somewhere in the interval of the
integration (assuming that the function is sufficiently smooth and actually has
a second derivative).
Repeated application of the above over each of the 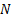 parts
of the overall integration results in the extended trapezoidal rule,
namely:
parts
of the overall integration results in the extended trapezoidal rule,
namely:
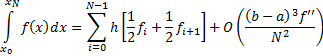
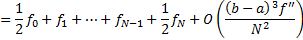
Here we have written the error estimate in terms of the
overall interval size 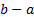 and
and 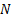 rather
than
rather
than 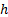 as usually
as usually 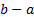 will
be fixed and
will
be fixed and 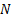 varied to
achieve a desired level of accuracy. This highlights that the accuracy of the
trapezoidal rule improves by a factor of
varied to
achieve a desired level of accuracy. This highlights that the accuracy of the
trapezoidal rule improves by a factor of 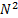 as
as 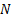 increases
(if the function being integrated is sufficiently smooth).
increases
(if the function being integrated is sufficiently smooth).
The trapezoidal rule is a two point formula (in the sense
that each underlying interval involves just two points, 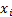 and
and 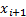 ) and is exact
for polynomials up to and including degree 1, i.e.
) and is exact
for polynomials up to and including degree 1, i.e. 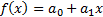 (i.e.
straight lines). We might therefore expect that there is a three point formula
that is exact up to polynomials of degree two (i.e. quadratics). This is indeed
the case, and it involves Simpson’s rule (here we use the convention
that
(i.e.
straight lines). We might therefore expect that there is a three point formula
that is exact up to polynomials of degree two (i.e. quadratics). This is indeed
the case, and it involves Simpson’s rule (here we use the convention
that 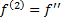 ,
, 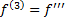 ,
, 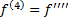 etc.
etc.
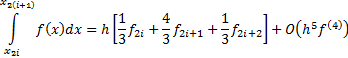
Classically, a variety of other formulae were developed that
fitted higher and higher order polynomials, e.g. Simpson’s 3/8 rule, Bode’s
rule etc., but in practice the (extended) trapezoidal rule has some subtle but
important facets which make it the starting point for many different numerical
integration techniques, see e.g. Press et
al. (2007). In particular, the error of the approximation which begins
with a term of order 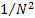 is entirely
even when expressed in powers of
is entirely
even when expressed in powers of 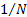 .
.
Suppose, therefore, that we evaluate the trapezoidal rule
with 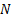 steps (i.e.
steps (i.e. 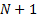 abcissae)
and come up with an answer
abcissae)
and come up with an answer 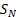 . Suppose we
repeat it with
. Suppose we
repeat it with 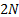 steps (i.e.
the
steps (i.e.
the 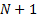 abcissae
previously used plus
abcissae
previously used plus 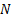 further ones
equally spaced between them) and come up with an answer
further ones
equally spaced between them) and come up with an answer 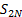 . Then, if the
function is sufficiently smooth, the leading error term in the second
evaluation will be one-quarter of the size of the leading error in the first
evaluation. We should therefore be able to test for convergence by repeatedly
doubling the number of terms evaluated, and we should be able cancel out
entirely the leading order error term using the combination:
. Then, if the
function is sufficiently smooth, the leading error term in the second
evaluation will be one-quarter of the size of the leading error in the first
evaluation. We should therefore be able to test for convergence by repeatedly
doubling the number of terms evaluated, and we should be able cancel out
entirely the leading order error term using the combination:
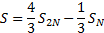
The residual error term is of order 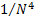 , the same as
Simpson’s rule; indeed it should not take long to realise that
, the same as
Simpson’s rule; indeed it should not take long to realise that 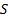 is
exactly the same as Simpson’s rule.
is
exactly the same as Simpson’s rule.
Various other refinements of this idea can be used to
improve convergence further, e.g. Romberg integration.
2. Alternatively, accelerated convergence
can relate to other more general methods of improving the convergence
properties of a series, i.e. where we approach the same end answer but with
fewer evaluations of the series.
For example, suppose we have two convergent series, say:
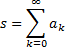
and
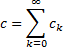
with the property that
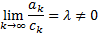
Then Kummer’s transformation indicates that a series with a
more rapid convergence to the same value is given by the following, see Abramowitz
and Stegun (1972):
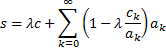
This becomes particularly helpful if 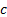 is
known already; useful cases include:
is
known already; useful cases include:
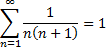
and more generally:
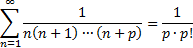
Other examples of convergence improvement are given in e.g. Weisstein (2015).